サイト・トップ |
ガスの科学ブログ |
ガスの科学目次 |
| 前の記事 | 97 |
次の記事 |
| 前へ | 目次順 |
次へ |
|
|
|
|
|||||||||||
| 5−13 ジュール=トムソン膨張 | |||||||||||
|
バルブを介して気体が噴出し、断熱自由膨張する時、気体の圧力は等エンタルピー線に沿って下がり、等エンタルピー膨張と呼ばれる。 前回のT-s線図に示したように、等エンタルピー線は、複雑な曲線になっており、圧力が下がると温度も変化していることが分かる。 この変化は、ジュール=トムソン膨張(JT膨張)あるいはジュール=トムソン効果(JT効果)として知られている。(ジュールとウィリアム・トムソンがJT効果を発見した経緯については →2−2 実在気体の科学 2−2−2 ジュール=トムソン効果に示した) |
|||||||||||
| ジュール=トムソン係数μを式で表すと次のようになる。(導出の手順は下記※) | |||||||||||
|
|||||||||||
| ここで、 |
|||||||||||
|
JT効果は、現象としてみると、気体の圧力が低下する時に、分子の距離が広がり、系が分子間力に対して仕事を行うために起こる。 理想気体では、分子間力が存在せず、JT効果がないことを述べたが、理想気体では、 気体の膨張は、 |
|||||||||||
|
|||||||||||
| 常温・常圧付近では、気体を理想気体として取り扱うことが多い。しかし、理想気体にはJT効果がなく(温度が変化しない)、図で言えば、等エンタルピー線が水平になるということである。T-s線図の右上の方にいくと、次第に理想気体に近づくということが読み取れるが、その領域は(産業ガス全般のハンドリングの範囲に対して)わずかしかない。 液化や、JT膨張を考える時、T-s線図上では、理想気体とみなせる範囲は非常に狭く、理想気体の状態方程式(ボイルの法則、シャルルの法則、アヴォガドロの法則など)はほとんど使えないことが分かる。常温・常圧付近で何かと便利に使われることの多い理想気体であるが、理想気体はJT効果がなく、分子間力がなく、液体にもならないので、ガス屋にとってはほとんど使えないモデルであるということが図からよく分かる。 |
|||||||||||
| ジュールとトムソンは、1852年にJT効果を発見、1861年にこれを理論化、50年後に、空気やヘリウムの液化に利用された。熱力学の偉大な業績は今日の様々な科学技術の基礎になっているが、これは科学の理論というだけでなく、実用性も高い技術でもある。しかし熱力学の先駆者の業績の多くが、ノーベル賞(第1回は1901年)よりも少し古いため、受賞は少ない。熱力学関連での受賞は、浸透圧を発見したファントホッフ、気体・液体の状態方程式を作ったファン・デル・ワールス、ヘリウムを液化したオネスなどが知られるだけである。 | |||||||||||
| ※ JT係数の式を変形して、(5-2)式を得る | |||||||||||
| JT係数の定義より | |||||||||||
|
|||||||||||
| 等エンタルピーの条件より | |||||||||||
|
|||||||||||
| したがって、JT係数は次のように変形される | |||||||||||
|
|||||||||||
| ここで | |||||||||||
|
|||||||||||
| であるから | |||||||||||
|
|||||||||||
| を用いて | |||||||||||
|
|||||||||||
| また、 | |||||||||||
|
|||||||||||
| と書くこともできるから、これを上式に代入して、P、Tで微分して、エントロピーを消去して次式を得る。 | |||||||||||
|
|||||||||||
これを(5-5)式に代入して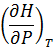 を消去すると を消去すると |
|||||||||||
|
|||||||||||
| ここで、 |
|||||||||||
|
|||||||||||
| これに膨張係数 |
|||||||||||
|
|||||||||||